[알고리즘]Recursion 개념

순환은 수학함수 계산에만 유용한가?

팩토리얼, 피보나치 수열, 최대공약수와 같은 수학함수 뿐만 아니라, 다른 많은 문제들을 recursion으로 해결할 수 있다.

문자열 뒤집기

def f(s):
    if len(s)==0:
        return
    else:
        f(s[1:])
        print(s[0],end='')

s=input()

f(s)

abcdef
fedcba

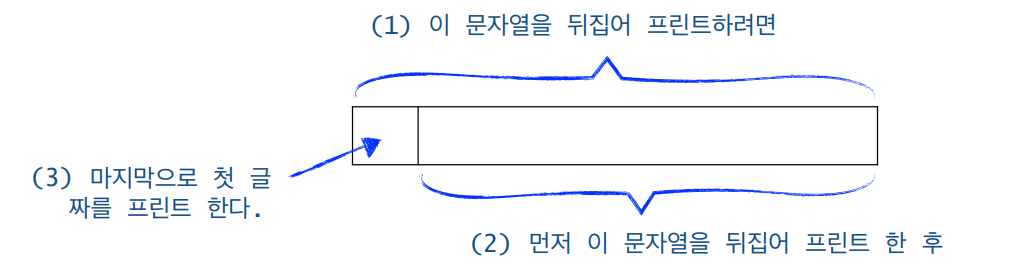
Base Case : 문자열의 길이가 0이면 출력을 하지 않고 return

재귀적으로 이해를 해야한다.
첫 번째 문자를 제외한 문자열을 뒤집어서 출력하고, 그 다음 제외한 첫 번째 문자를 출력한다. 이렇게 하면 문자열이 뒤집어서 출력된다.

2진수로 변환하여 출력하기

def fun(n):
    if n<2:
        print(n,end='')
        return
    
    fun(n//2)
    if n%2==0:
        print(0,end='')
    elif n%2==1:
        print(1,end='')

n=int(input())
fun(n)

33
100001

24
1100

Base Case : n이 0 또는 1이면 자기 자신을 출력하고 재귀함수를 종료한다.

n이 홀수라면 이진수의 제일 마지막 수는 1, 짝수라면 제일 마지막 수는 0이다.
따라서 n을 2로 나눈 몫을 이진수로 출력한 뒤, 나머지 연산을 통해 n이 홀수라면 1, 짝수라면 0을 출력하면 된다.

Recursion vs. Iteration

• 모든 순환함수는 반복문(iteration)으로 변경 가능
• 그 역도 성립. 모든 반복문은 Recursion으로 변경 가능하다.
• Recursion은 복잡한 알고리즘을 단순하고 알기쉽게 표현하는 것을 가능하게 한다.
• 하지만 함수 호출에 따른 오버헤드가 발생한다=프로그램 속도 면에서 느리다.
  (매개변수 전달, 액티베이션 프레임 생성 등)

Recursion의 설계

• 적어도 하나의 base case, 즉 순환되지 않고 종료되는 case가 있어야 한다.
• 모든 case는 결국 base case로 수렴해야 한다.
• base case는 하나가 아니고 여러개일 수도 있다.

그 중에서 중요한 포인트가 있는데 바로, 암시적 매개변수를 명시적 매개변수로 바꿔야 한다는 것이다.

순차탐색(명시적 매개변수)

def search(lst,begin,end,target):
    if begin>end:
        return False
    elif lst[begin]==target:
        return begin
    else:
        search(lst,begin+1,end,target)

시작 인덱스 begin을 명시적으로 선언하였다.
begin 값이 target과 같다면 begin을 리턴하고, 일치하지 않다면 begin+1 ~ target 까지 search 함수를 다시 호출한다.

최대값 찾기(명시적 매개변수)

def findMax(lst,begin,end):
    if begin==end:
        return lst[begin]
    else:
        return max(lst[begin],findMax(lst,begin+1,end))

시작 인덱스 begin을 명시적으로 선언하였다. 첫 번째 인덱스의 값과, 첫 번째+1 ~ 마지막 인덱스 까지의 최댓값을 비교하여 더 큰 값을 출력하면 lst의 최댓값이 출력된다.